Elevator pitch
The Mincer equation—arguably the most widely used in empirical work—can be used to explain a host of economic, and even non-economic, phenomena. One such application involves explaining (and estimating) employment earnings as a function of schooling and labor market experience. The Mincer equation provides estimates of the average monetary returns of one additional year of education. This information is important for policymakers who must decide on education spending, prioritization of schooling levels, and education financing programs such as student loans.
Key findings
Pros
Earnings can be explained as a function of schooling and labor market experience using the Mincer equation; this provides policymakers with important information about how to invest in education.
Due to the comparability of Mincerian results, individuals can make use of these results to help guide their personal decisions about how much schooling they should invest in.
Recent studies using the Mincer equation indicate that tertiary education, as opposed to primary education, may now provide the greatest returns to schooling; this represents a shift in the conventional wisdom.
Cons
The relationship between schooling and earnings does not necessarily imply causality.
Earnings functions provide private (i.e. individual) returns to schooling, whereas government/public costs and other benefits are needed to estimate social rates of return.
As economies become more complex and technological developments alter the demand for education, decades-old cross-sectional data may not be informative about returns to current investment decisions.
Author's main message
The Mincer equation suggests that each additional year of education produces a private (i.e. individual) rate of return to schooling of about 5–8% per year, ranging from a low of 1% to more than 20% in some countries. Globally, the returns to tertiary education are highest, followed by primary and then secondary schooling; this represents a significant reversal from many studies’ prior results. Policymakers can learn much from Mincerian results; for instance, further expansion of university education appears to be very worthwhile for the individual, meaning that governments need to find ways to make financing more readily available, and that high rates of return are found through investment in girls’ education.
Motivation
Private rates of return to schooling are undisputable. They are frequently used to explain individual behavior with respect to educational choices and to indicate productivity [2]. They can be used to analyze the distributional effects of education finance programs, which can guide public policy with respect to the design of programs and the crafting of incentives that promote both private and public educational investment. A good example is student finance, where returns to schooling estimates can be used to design student loan programs. They can help policymakers establish repayment rates, especially if income-contingent programs are adopted. This evidence can also be used to assess the prospective benefit of enrolling in post-secondary education, as the decision to enroll depends on the long-term outcomes of degree completion, earnings differences, degree completion, and field of study. As such, understanding how to assess returns to schooling and being able to appropriately apply those results to policy decisions is a critical skill for policymakers to have at their disposal.
Economists use so-called earnings functions to estimate returns to education, with the Mincer equation being arguably the most widely used in empirical work. It provides the estimations necessary to evaluate returns to schooling from a monetary perspective, and allows for the direct comparison of results. Empirical evidence on returns to investment in education provides useful indicators—typically in the form of projected future wages—that help individuals decide how to invest in their own human capital. These indicators can also be used as a basis for setting public policy with respect to investment in education.
Mincerian earnings functions have been estimated for a large number of countries and across many different demographic groups. The Mincer equation has become ubiquitous, to the point where people no longer reference the original source or may not even use the term “Mincerian” [3]. Its simple structure and parsimonious nature make the Mincer equation the most appropriate way to study earnings. On top of this, it is also a flexible model, which allows researchers to include other variables, while at the same time it delivers a precise method of modeling the relationship between earnings, schooling, and experience.
Discussion of pros and cons
The concept of schooling as a personal investment goes back to at least Adam Smith. Following the human capital revolution in economic thought in the 1960s, the worker’s educational level was analyzed extensively, with the microeconomics focus largely being on the returns to education. That is, the measure of the future economic benefits to an individual or society from increasing the amount of education undertaken. There are essentially two classes of estimation methods: one that uses the internal-rate-of-return procedure, and another that approximates this procedure by fitting an earnings function to individual data sets. The internal rate of return is found by setting the discounted value of costs and benefits over time equal to zero and finding the implicit discount rate, but this is not examined further in the present article as it is beyond the scope of the Mincer equation or other standard earnings functions.
The Mincer equation explains earnings as a function of schooling and labor market experience, giving a clear sense of the average monetary returns of one additional year of schooling. The rate of return to investment in schooling is presented in a simple and comparable format that permits estimates of the profitability of schooling, thus allowing people to use this information for investment decision purposes.
The interest in ascertaining the value of the investment in education has increased over time. Worldwide, education spending has increased from 3.6% of GDP in 1970 to more than 4.8% of GDP in 2011. At the same time, individuals and their families invest a significant amount out of their own pockets for tuition and other education-related expenses. The student’s foregone earnings represent the largest costs incurred by individuals and their families while studying. Is this massive investment in schooling justified? One way to analyze this question is to estimate the costs and benefits of the investment, for which the Mincer equation is ideally suited.
Although most rate of return studies attempt to estimate the returns to schooling for a country, region, or level of schooling, lately there has been interest in more disaggregated information such as returns for certain population groups categorized according to specific characteristic, e.g. ethnic, linguistic, religious groups, persons with disabilities, and so on. Estimating Mincer equations for different groups such as males and females or ethnic groups can be used to study the extent of labor market discrimination. Returns to schooling for women are used to justify further investments in girls’ schooling. Returns to schooling in developing countries are used to justify international goals for getting all children into school. In developed countries, the massive investments in higher education, rising tuition levels, and increasing student debt loads are calling into question the overall attractiveness of educational investment.
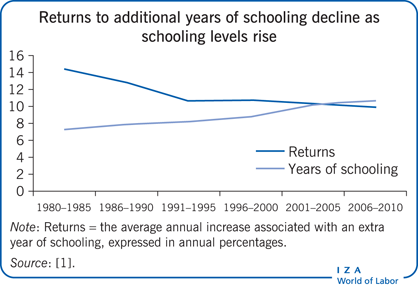
It should be noted that the relationship between schooling and earnings does not necessarily imply causality. Moreover, since earnings functions provide private returns to schooling, the only cost taken into account is the foregone earnings associated with attending school instead of earning a working wage. To obtain an estimate of the social return to schooling, one needs to identify other costs (e.g. government/public costs of education) and benefits outside of wages, such as health benefits. Moreover, despite the usefulness of rate of return estimates, rapidly changing conditions (i.e. technological developments and increasing overall economic complexity) degrade the value of using historical cross-sectional data to make current investment decisions. Another issue is that the simple Mincer equation estimates an average marginal rate of return; however, the rate of return can vary with the number of years of schooling, and can decrease over the working lifecycle and by cohort; as seen in the Illustration, the returns to another year of schooling change—typically decline—as the average level of schooling rises over time.
Interpretation of results from an earnings function
The form of the earnings function—that is, which variables to include and how they enter the equation—is important [4]. Researchers typically use hourly earnings as the dependent variable (the outcome of interest) in these calculations. However, the time frame over which earnings are measured is often determined by necessity: some data sets report annual earnings whereas others report weekly or hourly wages. Because individuals with higher levels of schooling tend to work more, the resulting return to schooling will be greater when using weekly or annual earnings than hourly earnings [5]. This must be kept in mind when constructing and interpreting the results from earnings functions.
Next to education, work experience is another important (explanatory) variable that accounts for the post schooling accumulation of human capital and therefore consequently affects earnings. Age is commonly used to approximate experience, though one must account for each individual’s number of years spent in school when doing so as this has an impact on the individual’s starting qualifications. In developing countries where children may not start school on time due to, for example, illness, cost, or distance, or when there is a high incidence of serial repeaters, there may be a bit of measurement error in using years of schooling to approximate experience. However, omitting experience would lead to biased results due to the relationship between experience and other relevant characteristics. In particular, experience and schooling are negatively correlated, i.e. when examining people of the same age, those with more years of schooling have less work experience. And both schooling and experience are positively correlated with earnings. This means that omitting experience could lead to an underestimation of the effects of schooling on earnings [6].
Moreover, one of the limitations of the Mincer equation is the assumption that returns to experience are the same at all levels of education. The problem of heterogeneous experience premiums is noted in the literature, but no agreed solution has so far appeared. Furthermore, experience not only captures on-the-job learning and the deterioration of skills, but also picks up institutional or contractual issues, such as when firms offer earning profiles that are skewed toward older workers in order to prevent shirking. In labor economics one speaks of the efficiency wage hypothesis, which argues that some managers may have an incentive to pay employees a salary above market rates in order to reduce the costs associated with turnover, especially in industrial sectors where the costs of replacing labor are high. Part of this incentive wage may be captured by the experience coefficient.
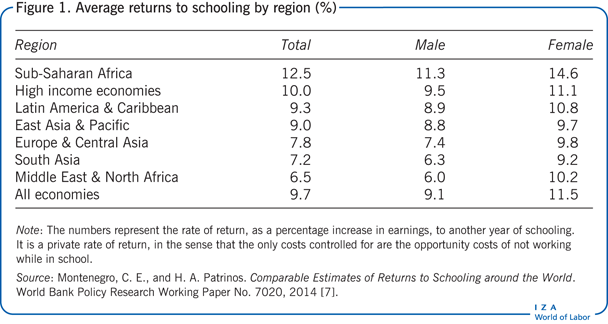
The interpretation issues that arise when reading the results of an earnings function are illustrated in the compilation of returns to schooling from 139 economies (Figure 1). The study shown is typical, in the sense that it uses representative, structured surveys and estimates earnings profiles using cross-section data. The first column shows the results for the typical Mincerian function with years of schooling as a continuous variable. The results represent workers with positive earnings in the labor market, which is a large sample. Overall, the returns to schooling are highest in sub-Saharan Africa, at 12.5%. Returns are also high in high-income economies, Latin America and the Caribbean, and East Asia and the Pacific, at 10%, 9.3%, and 9%, respectively. The lowest returns are found in the Middle East and North Africa, at only 6.5%. Overall, the global average return is just under 10% [7].
Figure 1 also shows returns by gender. On average, returns to schooling are significantly higher for women than for men. The lowest returns to schooling are for men in the Middle East and North Africa, at only 6%. The highest returns to schooling are for women in sub-Saharan Africa, at almost 15%.
Global estimates of the returns to schooling
Most studies that present compilations of returns to schooling suffer from problems of comparability due to data sample coverage and methodology. One common problem is that surveys may not accurately reflect population averages. Researchers also typically include many different independent (explanatory) variables in their models, which may affect estimates of the returns to schooling, and different studies rarely use the same models. The typical Mincerian earnings function uses a limited number of variables—earnings, schooling, and experience. But, some researchers add many other variables including sector of employment, region, and so on. They may also specify the variables differently, all of which makes comparability difficult. However, recent estimates provide results for a large number of countries, with one new compilation presenting comparable estimates of the private returns to schooling using 911 household surveys from 139 economies [7]. The study maintains a constant definition for the outcome variable, the set of control (independent explanatory) variables, the sample definition with respect to age, and the estimation method for all surveys represented in the sample.
Previous compilations of the literature suggest certain conclusions [7]:
The global average private rate of return to a year of schooling is about 10%. New evidence suggests that the return to another year of schooling (marginal return) is indeed positive, significant, and more concentrated around the mean than previously thought, at 9.7% overall [7].
The returns to schooling are higher in high-income economies and in sub-Saharan Africa.
The returns to schooling are higher for women than for men. Women receive a rate of return of 11.5%, compared to 9.6% for men [7]. (However, simply applying the Mincer earnings function for women may be biased, for instance, due to incorrect measurement of experience, selection due to the fact that women are less likely to be wage earners, and because women often have discontinuous labor force participation.)
Though the returns to schooling decline as the supply of schooling in a country increases, they tend to decline only modestly over time, by no more than two percentage points in a given decade, and actually much less than that in recent years. Using global data, returns to schooling are shown to have declined significantly over time, but at a much slower rate than has occurred with the expansion in schooling, especially since the late 1990s [7]. While the supply of schooling has expanded by almost 50% worldwide since 1980, the returns to schooling have declined by only 3.5 percentage points, or 0.1% per year. At the same time, the average length of schooling has increased by more than 3 years, or 2% per year worldwide. On average, another year of schooling leads to a reduction of the returns to schooling by one percentage point.
Determining the most valuable return to educational investment
Individuals invest in a level of education or a degree program, rather than in years of education. The Mincerian equation is a flexible specification. Years of schooling can be replaced with other variables to represent the levels of schooling (e.g. specific types of degree programs). These become “dummy variables” (variables with two values: 0 and 1) for each level of schooling. Since levels of schooling are sequential—that is, you must complete primary to enter secondary, and secondary to enter tertiary—the returns to schooling for each level also incorporate the benefit of previous levels of schooling.
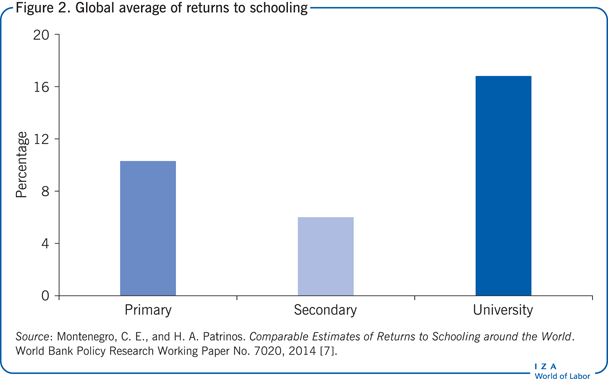
One of the long-standing conclusions from the literature is that returns to schooling are highest at the primary education level, but this is no longer considered true [7]. Globally, the returns to tertiary education are highest, followed by primary; the lowest returns are for secondary schooling (see Figure 2). On average, the returns to tertiary education are 17%, while they are 10% for primary education. The highest returns to tertiary are in Africa, at 22%, where one also finds the highest returns to primary schooling, at 13%. To some extent, the effect on primary education may be driven by an increase in compulsory education. That is, as countries develop and education systems expand, primary school becomes compulsory and universal, making it difficult or impossible to estimate returns to education, or to compare them to older workers who may have lower wages for other reasons.
Do skills gained from schooling or the acquisition of credentials lead to increased wages?
The earnings premium associated with level of education suggests that productivity increases as people acquire additional qualifications. An alternative view is that earnings increase with education due to credential effects. This refers to the idea that higher levels of schooling are associated with higher earnings, not because they directly raise productivity, but because they certify that the worker is likely to be productive. In this sense, education merely sorts workers according to their unobserved attributes; it does not necessarily augment their intrinsic productivity. For public policy reasons it is important to distinguish between the human capital (productivity) and screening hypotheses about returns to education. In very basic terms, these two hypotheses mean, respectively: schooling imparts skills that enhance productivity; hence, increases in earnings are due to the increased productivity brought about by investments in schooling (human capital); while the screening hypothesis maintains that employers select workers with higher qualifications to reduce their risk of hiring someone with a lower capacity to learn; in this case, higher earnings may not be due to productivity alone (screening). With these concepts in mind, if the only purpose of schooling is to sort prospective employees, then questions arise as to the appropriateness of public investment in the expansion or improvement of schooling.
The above debate is typically presented as an either/or argument. However, the observed correlation between education and earnings shows that, at an individual level, schooling does augment earnings. Some level of screening will likely exist, at least at the entry level, and perhaps also influence the decision to enroll. The earnings function can be used to examine the case for or against screening.
Most tests of the screening hypothesis use an earnings function. One test for screening examines returns for individuals with a completed education versus those who dropped out; if education serves as a signal (i.e. screening mechanism), then certification from a course should convey more information to prospective employers about an applicant’s ability than the number of years of schooling. Returns for completers would thus be higher than returns for non-completers. To examine the “weak versus the strong version of the screening hypothesis” one draws a distinction between employers paying irrational wages (i.e. wages that do not match the applicant’s qualifications or experience) at the initial hiring point (weak) versus those that continue paying such wages thereafter (strong). Most applications of the “weak versus the strong version of the screening hypothesis” do not find strong evidence of screening. A recent analysis that uses rigorous evaluation techniques to compare the earnings of workers who barely passed versus those who barely failed high school exit exams finds little evidence of diploma screening effects [8].
More rigorous tests of the screening hypothesis involve taking advantage of “natural experiments” such as changes in the school leaving age or college openings. By and large, while some evidence of weak screening is revealed, education is generally associated with higher earnings due to productivity rather than to screening. Thus, investment in schooling continues to be a worthwhile activity for individuals and societies to undertake [9].
The debate is ongoing about the external validity and causality of rate of return estimates. More conclusive evidence will emerge once data on the lifetime earnings profiles of beneficiaries of voucher programs can be obtained, as many of these programs use lotteries to assign places, thus giving researchers access to randomized data. In 1981, Chile introduced nationwide school choice by providing vouchers to any student wishing to attend a “voucher school” (essentially, a private school participating in the program, whereby the funding from the voucher would be used to pay the fees and tuition). Beneficiaries of the vouchers obtained more schooling and subsequently earned more than non-voucher students. Also, it is estimated that formal sector earnings are higher for lottery winners in Colombia’s large-scale government program which used a lottery to distribute scholarships for private secondary school to socially disadvantaged students.
Institutional factors have also been used to more precisely estimate the returns to schooling, including the effect of birth date. Those who are forced to remain in school because of their birth date and the school attendance law receive the same rate of return to education as those who voluntarily continue schooling.
Limitations and gaps
One of the perennial debates in educational economics is the extent to which returns to schooling are correlated with other factors, such as an individual’s ability, or if they are simply exhibiting the effects of selection. It could be that generally more able individuals choose to enroll in a study program or to undertake further years of schooling because they are more academically capable and will therefore benefit more from studying and subsequently be more likely to obtain a higher paying job. In such a case, individual self-selection is occurring, which may create an upward bias in the estimated rate of return to schooling. Also, educational institutions may offer enrollment to more able and easier to teach students, who are more likely to excel in the respective programs. Again, this would tend to introduce an upward bias in the returns to schooling.
Estimates of the returns to education based on advanced econometric techniques that control for different characteristics come to an average rate of return that is similar to the global average presented in most reviews. These more selective studies focus on the causality debate between schooling and earnings; they confirm that the effect of ability and related factors does not have a significant impact on the general results for returns to education. Still, more research on causality is needed.
More recent analyses, which exploit data that permit the disaggregation of earnings by years of completed schooling, have questioned the linear nature of the earnings function approach. Furthermore, due to ongoing and rapid technological progress, cross-sectional data based on observations from many years in the past may produce biased estimates of the returns to schooling. Some have even questioned whether it is still possible to interpret the coefficient on schooling as a rate of return [10]. For instance, some researchers argue that the literature following Mincer’s estimated returns to schooling using cross-sectional data assumes that younger workers base their earnings expectations on the current experiences of older workers. However, if prices (i.e. cost of schooling, for example, tuition associated with university) change over time and workers are able to at least partially anticipate these changes, then estimates of the return to different schooling levels based on cross-sectional data may not represent the ex-ante rates of return governing human capital investment decisions. Relying on past cohorts to assess current investment decisions requires several strong assumptions, such as stability of the economic environment and perfect certainty of future earnings streams. This is difficult in the current context, given that emerging evidence suggests that wage patterns have changed substantially over time, making it difficult to use cross sections to approximate lifecycle earnings. One solution could be to follow actual cohorts over their entire educational and employment lifecycles to measure their earnings patterns in order to estimate the returns to education.
Finally, private rates of return are globally applicable and useful. But, for many policy decisions, one needs to assess the broader social rates of return, which include government/public spending on the cost side and, among other things, monetary estimates of the benefits associated with an individual’s investment in education and their children’s education and health (e.g. declines in fertility, spouse’s health, job search efficiency, social cohesion, reductions in crime, and so on). These are not presented in this paper, since they require more data than is currently available for the vast majority of countries, and because they require estimation techniques that go beyond the capabilities of standard human capital earnings functions. The Mincer equation can incorporate social costs; more difficult is the inclusion of social benefits. Yet another difficulty is the absence of data for the many social benefits.
Summary and policy advice
Education remains a positive, significant, and profitable investment for individuals. On average, another year of education produces a private rate of return to schooling in excess of 5−8% a year. As such, there are few better investments one can make.
In a significant reversal, which is now seen worldwide, returns to schooling are highest at the tertiary level. This has important implications, as it will lead to an increase in demand for tertiary education and put pressure on policymakers to expand university education. This should not, however, come at the detriment of basic education, since primary education is a fundamental human service, and access to primary (and secondary) education is a prerequisite for entry into university.
While women may receive less pay than men—though the gender gap appears to be declining—an investment in education at all levels provides a greater payoff for women than for men. The policy implication from this is obvious. Countries need to continue efforts to invest in girls’ education, and must ensure that females complete their primary and secondary schooling. Because the payoff to university education is so high, efforts to get women into university represent a sound investment option, leading to overall efficiency gains and putting a further dent into the gender gap.
Returns to schooling have declined only modestly over a long period of time, despite massive worldwide investment in schooling, meaning that education continues to be a worthy investment. Policymakers would thus be wise to invest in basic education, continue to improve the quality of schooling, and to pursue sensible policies for the expansion of post-secondary education opportunities. For example, the high returns to higher education will entice individuals to demand this level of schooling. At the same time, high private returns suggest opportunities for cost-sharing and innovative financing models. Thus, governments can impose tuition and support those with financial constraints through student loans. Even better would be to use future resources—the graduates’ future earnings—to finance current education expansion. This would amount to income contingent loan programs that base future payments on the earnings of graduates. These types of loans mean that those who earn more will pay back their loan more quickly. Those experiencing difficulties finding high-paying jobs are allowed to repay their loans in smaller amounts, over a longer period of time, or even have their debts forgiven altogether.
The Mincer equation has clearly helped advance the fields of labor and educational economics. It has improved the understanding of the determinants of earnings, the rate of return to schooling, the demand for education, the impacts of discrimination, and the importance of labor market experience and on-the-job training. Moreover, the simple Mincer equation is now being used in other fields such as sociology and anthropology. The Mincer equation is thus a genuinely valuable tool for a wide-ranging group of researchers and policymakers; it should be relied upon extensively for determining educational return estimates and will continue to contribute to many other policy relevant fields in the future.
Acknowledgments
The author thanks two anonymous referees and the IZA World of Labor editors for many helpful suggestions on earlier drafts. Previous work of the author (together with George Psacharopoulos [1] and Claudio Montenegro [7]) contains a larger number of background references for the material presented here and has been used intensively in all major parts of this article.
Competing interests
The IZA World of Labor project is committed to the IZA Guiding Principles of Research Integrity. The author declares to have observed these principles.
© Harry Anthony Patrinos