Elevator pitch
Most of the data available to economists is observational rather than the outcome of natural or quasi experiments. This complicates analysis because it is common for observationally distinct individuals to exhibit similar responses to a given environment and for observationally identical individuals to respond differently to similar incentives. In such situations, using maximum likelihood methods to fit an economic model can provide a general approach to describing the observed data, whatever its nature. The predictions obtained from a fitted model provide crucial information about the distributional outcomes of economic policies.
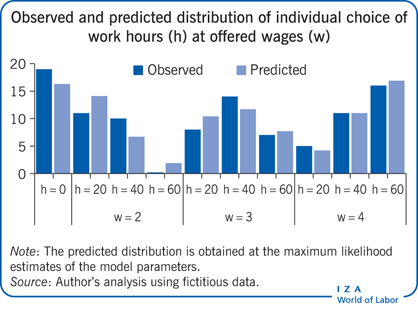
Key findings
Pros
Maximum likelihood methods enable the measurement of parameters of complex economic models even in the presence of complex sampling schemes.
Maximum likelihood can be used to analyze any kind of data, whether observational, experimental, or quasi-experimental.
By using all the information available in a sample, maximum likelihood methods produce measurements that are as “good as one can get” given the specified model.
Maximum likelihood methods allow the testing of all testable hypotheses that describe a given model.
Cons
Maximum likelihood methods require the specification of an economic model that properly describes the probability distribution of the events observed in the sample.
Using maximum likelihood requires assumptions about the distribution of unobserved components of the model.
If the modeling assumptions are not satisfied, the estimates will suffer from bias, which affects robustness.
Maximum likelihood methods rely on numerical methods to evaluate and maximize the likelihood.