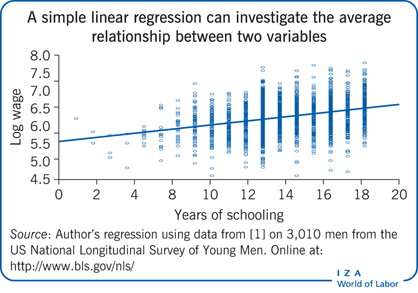
Elevator pitch
Linear regression is a powerful tool for investigating the relationships between multiple variables by relating one variable to a set of variables. It can identify the effect of one variable while adjusting for other observable differences. For example, it can analyze how wages relate to gender, after controlling for differences in background characteristics such as education and experience. A linear regression model is typically estimated by ordinary least squares, which minimizes the differences between the observed sample values and the fitted values from the model. Multiple tools are available to evaluate the model.
Key findings
Pros
Linear regression is a simple and convenient tool to establish an empirical relationship between one variable and a set of other variables.
Linear regression estimated by ordinary least squares is the “best linear predictor”: in a given sample, the estimated linear combination of regressors provides the closest approximation to the actual outcome.
Ordinary least squares works reasonably well even if the model is not perfectly specified.
Linear regression with ordinary least squares can provide a quick benchmark for more advanced methods.
Cons
Causal relationships are most valuable for policy advice and interventions, but interpreting a linear regression model as a causal relationship is challenging and requires strong assumptions.
Specification of a linear regression model is not always straightforward because there is no simple, hard rule that prescribes how to choose an appropriate specification.
Specification of a regression model requires care and statistical testing, particularly if estimates of interest appear very sensitive to the specification used or to the set of explanatory variables included.