Using linear regression to establish empirical relationships

The meaning of a linear regression model

A linear regression model assumes that the underlying relationship is linear. It may contain non-linear functions of explanatory variables or interactions between two variables, as long as the model is linear and additive in its coefficients. This allows a large degree of flexibility in the functional form. At the same time, the , which is the variable of interest, may be a transformed variable. For example, frequently log wages rather than wages are modeled, while squared years of experience is often included as an explanatory variable.

In its most basic role, the linear regression model provides the “best” linear approximation of one variable from a set of other variables. Essentially, this is a multivariate extension of a bivariate correlation coefficient and does not necessarily have any behavioral significance. That is, the regression model provides a means to summarize the data, rather than describing economic behavior or a causal relationship. In economics, a linear regression model is typically interpreted as approximating a population relationship describing the expected value of one variable given a set of others. This is referred to as a “conditional expectation.” For example, what is the expected wage of a female worker, given that she has finished high school and has ten years of working experience? This interpretation requires the correct functional form. Linear regression then decomposes the dependent variable into two components: a conditional expectation (a function of the explanatory variables) and a residual error term (not related to the explanatory variables).

In its most challenging role, the linear regression model describes a causal relationship. This requires strong assumptions and a good understanding of the underlying economic mechanisms. Causal relationships are most valuable for policy advice and interventions, but quite challenging to establish empirically. For example, while there is ample evidence that education and earnings are positively correlated, there is less consensus in answering the question to what extent higher earnings are caused by schooling [3]. It may simply be that individuals with more earnings potential (or “ability”) have chosen to acquire more schooling [4].

Interpretation of regression coefficients

When the regression model corresponds to a conditional expectation, each slope coefficient measures the expected change in the dependent variable following a one-unit change in the explanatory variable of interest, holding all other explanatory variables constant (the “ceteris paribus” condition). If the focus is on the relationship between one outcome variable and one regressor variable (in the example, the relationship between earnings and schooling), the other explanatory variables in the model act as control variables. Depending on the question of interest, the decision may be to control for some factors but not for all [5].

Sometimes the ceteris paribus condition is hard to maintain. For example, in the wage equation example, it may be that older people almost always have more experience. Although the regression coefficient in this case still measures the effect of age, keeping years of experience (and the other variables like gender) fixed, it may not be well identified from a given sample because of the high degree of correlation between the two variables (“collinearity”). In some cases, it is impossible to maintain the ceteris paribus condition—for example, when the model includes both age and age-squared. In that case, the two terms have to be interpreted together. An easy approach is to analyze the difference in expected outcomes (fitted values, predicted values) when age and age-squared change at the same time. Doing so shows that the effect of age on expected earnings is not constant but varies with age. More generally, the effects of explanatory variables can be allowed to vary over the observations by including additional terms involving these variables. For example, including an interaction term allows the effect of one variable to depend on the other. This way, the model can allow the effect of age on wages to depend on gender or schooling, for example. Thus, age might have different effects on earnings for men and women or for high school graduates and college graduates.

There are numerous challenges in identifying causal effects in empirical work [6]. Interpreting a regression model as a conditional expectation does not necessarily imply that its parameters can be interpreted as measuring causal effects. For example, it is not unlikely that expected earnings vary for married and unmarried workers, even after controlling for many other factors, but it is not very likely that being married causes people to have higher earnings. Rather, marital status is a proxy for a variety of observable and unobservable characteristics that also affect a person’s wage. Similarly, if you try to relate regional crime rates to, say, the number of police officers, you will probably find a positive relationship. That is because regions with more crime tend to spend more money on law enforcement and therefore have more police, not because the police are causing the crime.

If the desire is to interpret coefficients causally, the ceteris paribus condition must include all other (observable and unobservable) factors, not just the explanatory variables that are included in the model. Whether such an extended interpretation of the ceteris paribus condition makes sense—and whether a causal interpretation is appropriate—depends crucially on the economic context. Unfortunately, statistical tests provide very little guidance on this issue. Accordingly, caution is required in attaching a causal interpretation to estimated coefficients.

Ordinary least squares

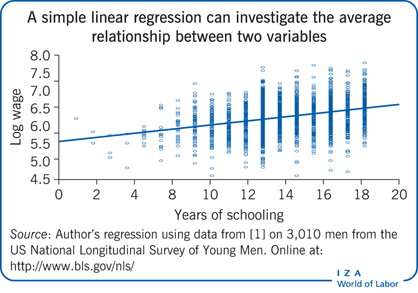
A linear regression model is typically estimated by OLS. In all cases, the OLS estimates are determined as the regression coefficients that minimize the sum of squared differences between the outcome variable and the linear combination of explanatory variables. When there is only one explanatory variable, this boils down to fitting a straight line through the observed scatter plot, as depicted in the Illustration. The regression line is chosen so as to minimize the sum of squared vertical differences between the fitted line (the solid diagonal line) and the observation points. In a multivariate setting, the regression model corresponds to a line in a more-dimensional space, but the intuition is similar.

The OLS estimator is a random variable whose outcome depends on the sample being used. The quality of the OLS estimator is judged by the distributional properties of the random variable. An important property is unbiasedness, which means that the expected value of the OLS estimator equals the true value in the population. When this result holds only for very large samples, the estimator is said to be consistent. Formally, this states that as the sample size grows, the estimator comes closer and closer to the true value. Another important property is efficiency, which means that the OLS estimator is the most accurate estimator given the available sample and the assumptions made. The accuracy of an estimator is reflected in its standard error. A small standard error indicates that the estimator exhibits little sampling variation (meaning that different samples will produce similar estimates), so that the corresponding effect is accurately estimated.

The OLS estimator in the linear regression model has good statistical properties provided that several assumptions are satisfied. Most important is that these assumptions impose restrictions on the relationship between the disturbance term and the explanatory variables. The strongest set of assumptions states that the disturbance terms are independent of all explanatory variables. This means that the unobservable variables affecting the outcome variable are not related in any way to the observed explanatory variables. Whether this makes sense depends crucially on what these unobservable variables (as collected in the disturbance term) are and what behavioral interpretation is attached to the model.

This strong set of assumptions leads to the Gauss–Markov theorem, which states that the OLS estimator is the “best linear unbiased estimator” for the unknown model coefficients. This means that, in repeated sampling, the OLS estimator is on average correct and that it is the most accurate estimator among all unbiased estimators that are linear functions of the dependent variable. Routinely calculated standard errors are appropriate in this case. One of the assumptions underlying this result is that the error terms in the model are independent drawings from the same distribution (independent and identically distributed). This imposes the crucial assumption that error terms are “homoscedastic,” that is, they all have the same variance, independent of the values of the explanatory variables in the model. This also imposes the assumption that two different error terms are independent of (and thus uncorrelated with) each other, which is implied by assuming that the sample is randomly drawn from a larger population.

The assumption of homoscedasticity is frequently violated, a case referred to as “heteroscedasticity.” For example, it may be that higher-educated workers have more variation in their unobservable variables affecting wages than do lower-educated workers. In that case, routinely calculated standard errors are incorrect, and the use of heteroscedasticity-consistent (robust) standard errors is an easy way to fix this [7]. With multi-level data (such as students within classes within schools), panel data (for example, data on the same individuals over ten years), or time series data (for example, data on aggregate monthly unemployment rates over a historical period) it is likely that error terms are correlated across different observations, due to serial correlation, group effects, unobserved (time-invariant) heterogeneity, or other factors. This problem can also be handled by using the OLS estimator in combination with standard errors that are robust to serial correlation and heteroscedasticity or by using alternative but related estimators like generalizes least squares [8], [9]. In summary, in most circumstances these assumptions do not affect the consistency of the OLS estimator, and violation of the assumptions can be handled using robust standard errors in combination with OLS [10].

Illustration of ordinary least squares estimation

To illustrate some of the issues discussed here, consider a sample of 3,100 men taken from the US National Longitudinal Survey of Young Men (also employed in [1]). This panel survey followed a group of men from 1966, when they were 14–24 years old, and interviewed them over several consecutive years up to 1981. This example uses labor market information on this group for 1976, meaning that it uses cross-sectional data. The dependent variable is the natural logarithm of a person’s hourly wage rate (log wage). Explanatory variables are years of schooling, years of labor market experience, and dummy variables for being black, living in the southern US, and living in an urban area. The example starts with a simple bivariate regression relating log wages to years of schooling (see the Illustration and specification 1 in Figure 1). Next, the model is extended by including years of experience and years of experience squared (specification 2). Finally, three dummy variables are included (black, southern US, and urban residence; specification 3).

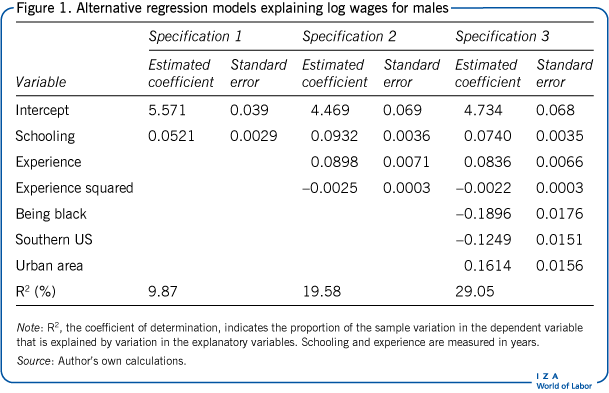
In specification 1, the estimated coefficient for years of schooling is 0.0521. This indicates that, on average, a man can be expected to have 5.3% higher wages for each additional year of schooling (see Figure 1). (Note that a 0.0521 increase in log wages corresponds approximately to a 5.3% increase in wages.) This interpretation does not control for other characteristics of the person. It simply estimates a person’s expected wage when all that is known is the number of years of schooling. The graphical representation of this relationship is depicted in the Illustration.

Specification 2 extends the model by including years of experience and its square. Years of experience squared is typically included to capture decreasing returns to experience. Controlling for differences in experience raises the estimated impact of schooling to 0.0932, or about 9.8%. This is because people with more years of schooling tend to have less experience. As a result, the estimated coefficient for schooling in specification 1 is partly capturing the effect of lower years of experience for highly educated men. The estimated coefficients on experience reveal that one additional year of experience raises expected wages by about 9% initially, dropping to about 4.2% for ten years of experience, keeping years of schooling fixed in both cases.

Specification 3 extends the model with dummy variables for race/ethnicity and residence. Wages are lower for black men and for men living in the south. Again, this specification affects the estimated effect of schooling, which is now about 7.4% a year. For two men of the same race, same residence (captured by “southern US” and “urban area”), and same years of experience, this means that wages are expected to be 7.4% higher when one man has one more year of schooling than the other.

As long as the model is very explicit about the characteristics it controls for, each of the three specifications can be interpreted as just described. If, however, the coefficients in specification 3, or in an even more extended specification, are the ones that are of interest, the estimates for specifications 1 and 2 are biased since they are not estimating the correct effect. This is referred to as “omitted variable bias,” as will be discussed below.

Figure 1 also reports the standard error with each estimated coefficient. The standard error can be used to judge the precision of the estimates and to test restrictions on the true population coefficients. For example, if the intention is to test whether, in the population, being black has an impact on a person’s wage, then one can calculate the ratio of the estimated coefficient (–0.1896) to its standard error (0.0176), which yields a value of –10.8. Normally, values that are outside the interval of –2 to +2 are interpreted as a rejection. This means that in this case, the null hypothesis—being black has no effect on a person’s wage—is strongly rejected.

Crucial assumptions

The Gauss–Markov assumptions impose that the explanatory variables are independent of the error terms. This is a very strong requirement and likely to be violated when non-experimental data are used. A weaker alternative imposes “conditional mean independence,” whereby the expected value of the error term is zero, conditional on the explanatory variables included in the model [5], [6]. It is typically expected that adding more control variables increases the likelihood that this assumption is appropriate. Under the assumption of conditional mean independence, the OLS estimator is consistent, and the regression model can be interpreted causally.

To illustrate this point, one can go back to the example of estimating the returns to schooling as a causal question, trying to estimate the impact on workers’ earnings (on average) of an exogenous change in their schooling. Put differently, what is the expected wage differential between two men who have different amounts of schooling but are otherwise identical? As shown in the empirical example above, the advantage of a linear regression model is the ability to control for other factors (see Figure 1). Once differences in these control variables are accounted for, the unobservable variables affecting earnings are less likely to be correlated with schooling. For example, in estimating the relationship between earnings and schooling, one might want to control for any other factor that makes individuals with higher levels of schooling different from those with lower levels of schooling, such as demographic and family background characteristics or proxies for ability, such as test scores.

In econometrics, the logic just described is often formulated in terms of omitted variable bias. The OLS estimator for the coefficient on schooling is biased (and inconsistent) if variables that are omitted from the regression are correlated with schooling. Such variables are often referred to as “confounding variables.” Accordingly, a key challenge in empirical econometrics is to find an “appropriate” specification for a regression model—one that includes all crucial control variables and confounding variables and that has the correct functional form. Alternative approaches, such as instrumental variables estimation, are available to address the problem of omitted variable bias, but these approaches impose strong conditions.

Specification search and testing

Regrettably, there is no simple rule for determining the most appropriate model specification in a given application. Because specification is difficult, only a limited amount of reliable data is available, and theories are often highly abstract or controversial. Specification of a model is thus partly an imaginative process for which it is hard to establish fixed rules. (For a discussion of specification searches in practice, combined with the “ten commandments of applied econometrics,” see [11], Chapters 5 and 21.) In practice, most applied researchers start with a reasonable model specification that could be appropriate and then test whether restrictions imposed by the model are correct and restrictions not imposed by the model could be imposed. In the first category are misspecification tests for omitted variables, but also for homoscedasticity and zero serial correlation in the error terms. In the second category are tests of parametric restrictions, for example, that one or more explanatory variables have zero coefficients.

Besides formal statistical tests, other criteria are sometimes used to select a set of regressors. First of all, the coefficient of determination (R2 ) measures the proportion of the sample variation in the dependent variable that is explained by variation in the explanatory variables. By construction, OLS provides the best linear approximation (for a given set of explanatory variables). For the specifications displayed in Figure 1, the R2 varies from 9.9% to 29%, depending on the specification. These values indicate, for example, that 9.9% of the variation in log wages can be explained by variation in schooling alone, while 29% can be explained by variation in schooling, experience, race, and two residence indicators. This is a typical order of magnitude for an empirical wage equation.

If the model were to be extended by including more regressors, it is clear that the explained variation would never decrease and thus that the R2 would never decrease. Using the R2 as the criterion would thus favor models with as many explanatory variables as possible. This degree of expansion is certainly not optimal, however, because with too many variables the model would not be able to say much about the coefficients, as they might be estimated inaccurately. Because the R2 does not “punish” the inclusion of many variables, it would be better to use a measure such as the “adjusted R2 ,” which incorporates this trade-off between goodness-of-fit and the number of regressors employed in the model.

A wide variety of statistical tests are available to test the restrictions imposed by the linear regression model. These include tests for heteroscedasticity, such as the Breusch-Pagan test and the White test; tests for serial correlation in time series data, such as the Durbin–Watson test and the Lagrange Multiplier test; and tests for functional form, such as Ramsey’s RESET test [2], [9]. In general, it is recommended to perform enough such tests to be able to argue that the linear regression model is reasonably well-specified and that statistical inference is not obviously misleading (for example due to the use of incorrect standard errors).

Once a linear regression model is specified and estimated, it can be used for generating predictions. For example, one can predict the wage of a worker with certain background characteristics. Further, the model can be used to test economic hypotheses. For example, one can test whether there is a significant difference between wages for male and female workers after controlling for differences in education and experience. This is done by means of the t-test or, more generally, the Wald test. These tests are based on comparing the coefficient estimates with the hypothesized values, taking into account precision of the estimates (standard errors). For robustness, tests are preferably based on heteroscedasticity-consistent standard errors. If the regression model has a causal interpretation, it can also be used to answer “what if” questions. That is, it can generate predictions for the outcome variable after changing one or more of the explanatory variables to reflect, for example, a policy intervention.