Relevanz des Themas
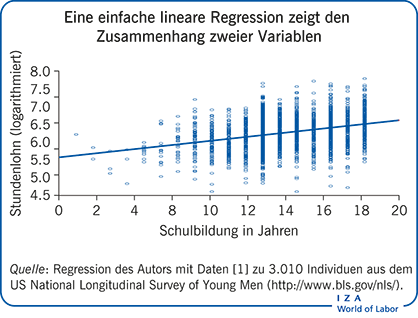
Eine Herausforderung für Sozialwissenschaftler besteht darin, Zusammenhänge zwischen Variablen zu identifizieren und dabei die Wirkungen anderer Einflussgrößen herauszurechnen. Ein Anwendungsbeispiel ist die Ermittlung von Geschlechterlohnunterschieden: Hier sind Unterschiede etwa beim Bildungsstand oder der Berufserfahrung zu berücksichtigen. Dazu dient die lineare Regression, die typischerweise auf der statistischen Methode der kleinsten Quadrate basiert. So lassen sich die Unterschiede zwischen den Stichprobenwerten und den angepassten Werten des Modells minimieren. Zur Auswertung stehen verschiedene Verfahren zur Verfügung.
Wichtige Resultate
Pro
Die lineare Regression ist ein praktisches statistisches Werkzeug, um empirische Zusammenhänge zwischen Variablen zu ermitteln.
Mittels der Methode der kleinsten Quadrate liefert die Schätzung der Regressoren den „besten linearen Prädiktor“, also die bestmögliche Annäherung an das tatsächliche Ergebnis.
Die Kleinstquadratemethode ist auch dann praktikabel, wenn das Modell nicht perfekt spezifiziert ist.
Lineare Regressionen dienen als einfache Benchmark für komplexere Methoden.
Contra
Aussagen über Kausalzusammenhänge, die für die Politikberatung besonders wertvoll sind, lassen sich mit linearen Regressionsmodellen meist nur unter sehr starken Annahmen treffen.
Die Erstellung eines linearen Regressionsmodells wird dadurch erschwert, dass es keine klaren Regeln für die Auswahl einer geeigneten Spezifikation gibt.
Sorgfältige statistische Tests sind insbesondere dann notwendig, wenn die Zielvariable sehr sensibel auf Veränderungen der Modellspezifikation bzw. der erklärenden Variablen reagiert.