Elevator pitch
A strong association between incomes across generations—with children from poor families likely to be poor as adults—is frequently considered an indicator of insufficient equality of opportunity. Studies of such “intergenerational persistence,” or lack of intergenerational mobility, are concerned with measuring the strength of the relationship between parents’ socio-economic status and that of their children as adults. However, reliable measurement requires overcoming important data and methodological difficulties. Moreover, the association between equality of opportunity and common measures of intergenerational persistence is not as clear-cut as is often assumed.
Key findings
Pros
Intergenerational income elasticity, a measure of inequality transmitted between generations, is related to a well-developed conceptual framework.
Comparisons of intergenerational income persistence across countries, localities, and time reveal settings where intergenerational links are weaker.
The impacts of poorly measured parental income on estimates of intergenerational elasticity are clearly understood.
Correlations between rank positions in the income distribution, which are unrelated to the particular distribution, may be a purer measure of persistence than elasticity. Researchers are developing other measures which can capture the size and direction of mobility.
Cons
Not all mechanisms driving intergenerational persistence are necessarily clearly related to fairness and equality of opportunity.
Data requirements for reliably comparing estimates of intergenerational mobility are stringent, resulting in considerable uncertainty.
Intergenerational elasticity assumes that the intergenerational relationship is constant across the income distribution and therefore is affected by changes in inequality between generations.
The properties of new measures of intergenerational persistence are less well understood.
Author's main message
Measures of intergenerational mobility, such as intergenerational elasticity, help paint a broad picture of intergenerational inequalities. However, data limitations introduce biases, and any discussion of optimal intergenerational persistence entails value judgments, which must be clearly articulated. By using new measures and data, and comparing intergenerational persistence across countries, time, and localities, researchers have begun to develop a more nuanced picture of intergenerational persistence and the mechanisms driving it. That is critical for identifying the most effective policy levers to apply.
Motivation
Studies of intergenerational persistence are concerned with measuring the strength of the relationship between the socio-economic status of parents and the socio-economic outcomes of their children as adults. A strong association between incomes across generations (intergenerational income persistence) indicates that children from a poor family are likely to be relatively poor as adults and that the elite positions in society are closed to most people.
Strong intergenerational persistence is frequently considered an indicator of insufficient equality of opportunity. It is difficult, however, to distinguish the reasons behind differences in economic success. For example, if children from higher-income families put in more effort than children from other socio-economic groups, an association in outcomes across generations might not necessarily violate principles of equality of opportunity and may even be desirable in a meritocratic society that rewards effort. Thus policymakers must understand that any assertion about the optimal level of intergenerational persistence is not value-free.
Comparisons of levels of persistence across countries and over time are used for putting estimates of intergenerational mobility in perspective. But for these comparisons to be based on reliable estimates, it is essential to consider some important methodological issues.
Discussion of pros and cons
The standard measure of intergenerational persistence
Intergenerational persistence can be measured in a variety of ways using various measures of socio-economic status. Among other measures, researchers have considered intergenerational links in family income, individual earnings, social class, occupational status, and education [2]. The most commonly used economic measure of intergenerational persistence links the earnings of fathers and their adult sons, although the combined incomes of parents and correlations with maternal income or daughters’ income are increasingly being taken into account.
The standard measure of intergenerational income persistence is obtained from a simple linear regression of children’s logarithmic income on parents’ logarithmic income. The slope coefficient, referred to as beta, gives an estimate of the intergenerational elasticity of children’s income with respect to their parents’ income. For example, say that one father had twice the income of another father. The wealthier father’s child would then have 50% more income than the child of the poorer father if the estimated statistic is 0.5, 20% more if it is 0.2, and so on. If the elasticity is zero, that means that a child’s adult income is not related at all to parental status, and so the best guess of a child’s adult income would be to take the average for the child’s cohort.
Data limitations in measuring intergenerational elasticity
An estimate of intergenerational elasticity is only as good as the underlying data on which it is based. Ideally, the intergenerational elasticity would be measured in terms of the parents’ and children’s permanent income (expected long-term average income), since permanent income has the strongest impact on consumption and the closest link to well-being. In recent years, much has been written about the potential biases arising from the use of imperfect data. The sources of estimation biases are measurement error in the recording of parental income and the sensitivity of estimates to the lifecycle [2].
Measurement error can lead to underestimates in the intergenerational elasticity of children’s income with respect to parents’ income. Early research on intergenerational persistence was based on survey datasets that often yielded error-ridden measures of income. Even when the survey income data were accurate, these measures were only weak predictors of long-term income, which is the variable of real interest. Simulations show that using a single year of earnings data can underestimate intergenerational persistence by 50% [1]. Two solutions have emerged.
One is to average fathers’ earnings over several periods to better approximate permanent income and to reduce the influence of measurement error.
A second solution is to use administrative data from tax records. Tax records have the dual advantage of being accurate records of income, assuming that tax evasion is not widespread, and they are available over a longer period, so that lifetime income can be better approximated. So far these sources have been primarily exploited for the Nordic countries, Canada, and, very recently, the US.
When lifetime measures of income are not available, it is important to measure the income of both generations at an age when their earnings are representative of earnings over their entire career; otherwise, lifecycle bias can affect the estimates. If the adult child’s earnings are observed at too young an age, the degree of intergenerational income persistence will be underestimated. Young people with a high level of educational attainment (who are likely to be from wealthier backgrounds) will not yet be established in their careers, making it appear that their earnings are more weakly linked to their parents’ earnings than they would be if the adult child were older. Recent explorations of UK data show intergenerational elasticity rising from just above 0.2 when measured at the age of 26 to close to 0.5 when measured at the age of 42 [3].
The standard measurement approach requires information on parental incomes and on children’s incomes in adulthood, some 20–30 years later. These data are not always available. It is more common to have sources of good information on adult children, which also contain retrospective information on fathers during the respondents’ childhood or teenage years. However, the quality of such retrospective data on income may be suspect, or the data may not be available at all. Retrospective information on occupation is less problematic (for example “What was your father’s occupation when you were age 14?”) and has been used in studies of the links between social classes across generations.
Two-sample instrumental variable approach
When information on the father’s earnings is not available, intergenerational persistence can be estimated using information on the father’s occupation, especially when combined with information on other characteristics such as education and age. Researchers can look to another dataset from the period when the child was growing up to see the average earnings of fathers with the same occupation and other characteristics. These data can be used in a regression model as a proxy for the father’s actual earnings.
This approach, known as the two-sample instrumental variable approach, was first used in comparisons of Sweden and the US. Since then, it has been used to expand the number of countries for which estimates of intergenerational persistence are available. The two-sample instrumental variable approach can potentially overstate intergenerational income persistence if the characteristics that are used to predict the father’s income are also related to the child’s outcomes. An example would be if the children of lawyers benefit from their father’s connections as well as his high earnings. Comparing studies that use this approach and studies that use a time-averaging approach on US data finds that estimates using the two-sample instrumental variable approach are about a third larger than estimates based on time-averaging of observed paternal earnings over a five-year period [4], [5].
It is important to stress that intergenerational elasticity does not measure the causal relationship between incomes across generations; the intention is not to find out how the child’s income as an adult would respond to a change in the parents’ income, everything else held constant. Rather, measures of intergenerational persistence provide a summary measure of intergenerational inequalities, assessing how children’s outcomes vary with parental income and all the other factors that can vary alongside it, such as parents’ education, family culture, motivation, and child’s ability.
One helpful comparison is with the Gini coefficient of cross-sectional income equality, where 0 describes the situation where national income is equally shared across the population and 1 describes the extreme case where all national income is held by one individual. The Gini coeffcient provides a summary measure of the extent of cross-sectional inequality, but it does not provide any information about its source. The intergenerational elasticity measure performs a similar function for intergenerational inequality.
A framework for analyzing the routes to intergenerational income persistence
The Becker–Tomes model provides a framework for analyzing the routes to intergenerational income persistence. The model starts with the idea that parents care about both their own consumption and that of their children as adults. Children’s adult incomes are determined by endowments, which are present in the individual without any cost, and by investments made in their education and skills. Endowments are to some extent inherited: on average, richer parents have better-endowed children. Because endowments are rewarded in the labor market, endowments account for some of the association between parents’ and children’s incomes. Investments can also depend on family income if children (or their parents) cannot borrow to support further education. If there are such credit constraints, the children of poorer parents will receive too little education, and intergenerational persistence will be inefficiently high. Researchers have therefore searched for evidence of credit constraints. The evidence for their existence has been mixed. Some analysts find evidence that money matters in itself [6], while others argue that financial credit constraints are not relevant in driving further education decisions, although they may be relevant at earlier ages [7].
The Becker–Tomes model therefore illustrates the difficulties of interpreting estimates of intergenerational persistence because inherited characteristics mean that intergenerational elasticities would be expected to take a non-zero value. In that case, how high is too high? Researchers have tried to answer this question by comparing intergenerational mobility between countries and regions and over time. The idea is that any intergenerational persistence that stems from endowments (for example, hereditary aspects) should be broadly constant across countries and localities. Thus, comparing international mobility in this way enables assessing which societies have relatively strong and which have relatively weak intergenerational persistence.
Comparisons of intergenerational elasticities across countries and localities
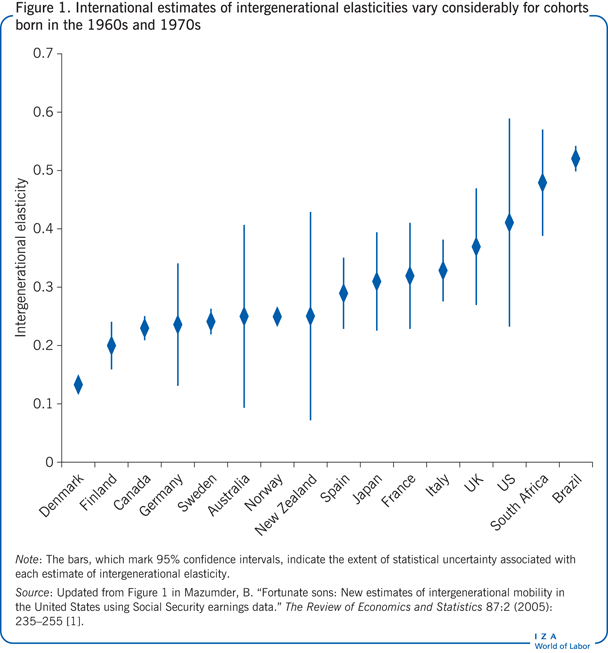
Figure 1 displays estimates of intergenerational elasticities for 16 countries, based on a literature survey conducted in 2013 [1] and updated in 2014. From that research, one estimate was chosen for each country. Selection was based on estimates obtained using the most comparable methods and cohorts. (One exception is the UK, whose estimate is an average from two studies.) Showing a range of estimates instead of selecting just one might have exaggerated the degree of uncertainty for countries for which there are more research studies. Additionally, it seems misleading to include estimates that are not comparable. In most cases, the selected estimates are based on data that have been averaged over several years. Where such estimates are not available, the two-sample instrumental variable method was used, and estimates were reduced by 0.75 to adjust for the potential upward bias of estimates derived using this method.
To give a sense of the reliability of the estimate chosen, the extent of statistical uncertainty associated with each estimate was also calculated. The degree of uncertainty is shown by the bars in Figure 1, which mark the 95% confidence interval (meaning that there is a 95% probability that the true value of the intergenerational elasticity is contained within the interval estimate). It is clear from Figure 1 that for some countries, particularly Australia, New Zealand, and the US, there is considerable uncertainty about whether the chosen estimate shows the true level of intergenerational elasticity. The reason for the greater uncertainty is that these estimates are drawn from very small samples. Despite the care taken in choosing the estimates, they may still generate controversy, as they depend in part on how the underlying research studies are interpreted. For example, the estimate for the UK displayed here differs from that in [8], and there has been recent disagreement over some new estimates for the US. Figure 1 relies on an older estimate of intergenerational persistence [4], which puts the US estimate shown here in the middle of the range of methodologically acceptable estimates.
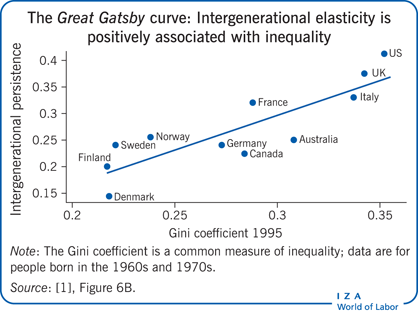
Comparisons of intergenerational persistence have been used to draw powerful policy conclusions. For example, two studies have taken estimates of intergenerational persistence from the literature and plotted them against Gini coefficient measures of cross-sectional inequality at a particular time, as in the Illustration [2], [8]. The resulting Great Gatsby curve indicates that in societies with high levels of income inequality, the extent of intergenerational persistence is higher. US government advisor and academic economist Alan Krueger called this relationship “the Great Gatsby curve,” after the novel by F. Scott Fitzgerald depicting social stratification in American society.
Of course, as is frequently noted, correlation does not imply causality. A positive association between cross-sectional inequality (Gini coefficient) and intergenerational inequality does not mean that narrowing the income distribution will promote intergenerational mobility. There could be many other variables associated with inequality that could be driving this result. In addition, as implied by the previous discussion of the uncertainty surrounding these estimates, there will always be concerns that the estimates are not fully comparable.
If there were a causal relationship, intergenerational persistence would be expected to rise for cohorts affected by rising income inequality. As Alan Krueger has asserted: “[P]ersistence in the advantages and disadvantages of income passed from parents to children...[will] rise by about a quarter for the next generation as a result of the rise in inequality that the US has seen in the last 25 years.” However, the rise in the US Gini coefficient began more than 30 years ago, so its impact would be expected to already be manifested in the trend in intergenerational income mobility. So far, however, evidence is inconsistent, with researchers finding rising, falling, and flat trends in intergenerational income persistence. In the UK, there is evidence of a rise in intergenerational persistence as inequality rose during the late 1970s and 1980s [9]. However, the evidence is based on children in just two week-long birth cohorts, making it hard to infer trends.
An alternative approach is to look at local areas within the US [10]. This approach has the advantage over the international Great Gatsby curve of holding constant country-level effects (and therefore of controlling for the fact that societies differ in many ways), as well as macroeconomic and other time-varying factors that could influence national trends. The study relates the extent of intergenerational persistence to inequality at the local level and to several other local characteristics, such as racial mix, family structure, and extent of migration. Thus, the study is able to distinguish the impact of inequality from that of other factors. The study also finds an association between cross-sectional and intergenerational inequality, although not for every measure. In summary, narrowing the income distribution is likely to reduce intergenerational inequality, but it is hard to say by how much.
Alternative measures of intergenerational persistence
So far, the discussion has focused entirely on intergenerational income elasticity. One appeal of the elasticity measure is that it follows directly from the Becker–Tomes model for analyzing the routes to intergenerational income persistence, which eases its interpretation. That is one reason why this statistic is estimated so frequently. However, intergenerational elasticity does have limitations compared with other measures of intergenerational persistence. For example, intergenerational elasticity is mechanistically affected by changes in the income distribution. Thus, if inequality is growing, so that it is greater in the adult child’s generation than in the father’s, this change in inequality will automatically show up as a higher intergenerational elasticity. This creates problems with making comparisons across countries and in interpreting the Great Gatsby curve.
An alternative measure of intergenerational persistence is the Pearson correlation of parents’ and children’s incomes, which adjusts for differences in income inequality between the two generations, by multiplying intergenerational elasticity by the ratio of the standard deviation of parents’ incomes to the standard deviation of children’s incomes. However, this is only one measure of the distribution of income. A recent review argues for more use of the Spearman rank correlation as a measure of intergenerational mobility [11]. This measure captures the correlation in income ranks completely independently of any changes in the distribution of income between the two generations. For example, a Spearman rank of 1 indicates that sons exactly mimic their fathers’ rank in the income distribution.
The rank correlation is closely related to transition matrices. Transition matrices are derived by dividing the income distributions of parents and adult children into equal numbers of quantile groups, for example quintiles, and noting the proportion of adult children from each parental income quintile who finish in each quintile of the adult children’s distribution. If all the children who begin in a particular parental income quintile remain in the same income quintile as adults, there is complete intergenerational immobility (all cells in the leading diagonal equal 1, and the others equal 0). If the starting income quintile has no effect on the destination quintile, there is complete intergenerational mobility (all cells in a given parental quintile equal 0.20). The rank correlation takes this measure to the limit by extending the number of categories to equal the number of observations in the sample.
Transition matrices are an improvement over the other measures mentioned so far because they clearly show the source of the intergenerational mobility. They can also indicate whether the effect varies at different levels of income and in different directions—whether the direction of mobility and the distance vary at different levels of income, showing whether children are moving up or down the income distribution and by how much.
Non-linearity in mobility patterns and estimates of the direction of mobility and the distance are of increasing interest to researchers. A recent study estimates measures of directional rank mobility for Canada, Sweden, and the US, along with intergenerational elasticities and correlations [12]. Directional rank mobility estimates what share of families is moving a particular distance in a given direction. For example, it calculates the probability of a child with parents in the bottom fifth of the income distribution rising to the top fifth.
The estimates of intergenerational elasticities for these countries broadly confirm the results in Figure 1: intergenerational persistence is higher in the US than in Canada or Sweden. However, measures of the Pearson correlation are very similar across the three countries (between 0.22 and 0.26), while estimates of the rank correlation show similar intergenerational links for the US and Sweden and slightly weaker links for Canada. In addition, less variability is found in correlations than in elasticities [3]. As individuals age, intergenerational rank correlation between parents’ income and adult children’s income increases only slightly, while intergenerational elasticity rises strongly. Measures of directional rank correlation reveal that the US has low levels of downward mobility from the top, implying that members of the elite in this high-inequality society seem to be better at maintaining their children’s position.
Limitations and gaps
Researchers are becoming increasingly aware of the empirical limitations of the intergenerational elasticity measure as well as of the difficulties in interpreting the findings. As a result, new measures are increasingly being used in empirical research. However, the intergenerational elasticity has its advantages. It relates clearly to an established model of how households behave, and researchers have a solid understanding of its behavior when data are weak or incomplete and have techniques for estimation using such data. To continue to advance the literature, researchers now need to develop a similar understanding of the new measures they are using. This task is harder because the measures are less standard, but the results are likely to prove very fruitful. More needs to be learned about the behavior of these estimates when the available data are not ideal.
It remains an unresolved question, however, whether researchers should always use rank measures and ignore the influence of the income distribution. More inequality means that the consequences of intergenerational persistence are more when each rung on the income ladder is further apart, this point is lost when rank correlation is used.
Strong assertions have been made on the basis of the association between cross-sectional inequality and intergenerational income persistence. However, there are substantial gaps in knowledge. The validity of the Great Gatsby curve has been questioned, and even if its validity is accepted, its drivers are not fully understood. It seems likely that some of the positive association between persistence and inequality comes from a mechanistic association between the two measures. But when evidence from new studies looking at local mobility [10] is combined with the finding that credit constraints matter [8], the results suggest that this mechanistic relationship does not show the full picture and that inequality does affect intergenerational persistence. More work is needed, in particular in bringing together the evidence from different approaches.
It is frequently claimed that high intergenerational persistence has implications for economic efficiency if the talents of children in poorer families are underdeveloped or underutilized. However, the optimum level of intergenerational mobility cannot be known a priori. Additional insight is gained by looking beyond headline measures of intergenerational mobility to understand the mechanisms that drive them.
Summary and policy advice
Knowledge of how to estimate intergenerational income persistence has grown considerably over the past 25 years. Although perfect data are rarely available, researchers now understand the most common biases that arise when measuring intergenerational elasticity and have techniques for dealing with them. Recently, researchers have begun to move away from the straightforward measure of intergenerational elasticity and are developing a more nuanced picture of intergenerational persistence. Because it is difficult to know what the optimum level of intergenerational persistence should be, researchers are increasingly comparing levels across countries, time, and localities. These comparisons are providing new insights into the mechanisms that drive intergenerational mobility and are identifying what could be the most effective policy levers to pull.
These are welcome developments because the extent to which advantage and disadvantage persist across society is a vital element of the shape of society, affecting its vibrancy and its success.
Acknowledgments
The author thanks two anonymous referees and the IZA World of Labor editors for many helpful suggestions on earlier drafts. This paper has drawn in part on a draft chapter written for the Brookings Foundation/Human Capital and Equality of Opportunity Global Working Group Workshop on “Equality of Opportunity: The Facts and the Philosophy” in September 2014.
Competing interests
The IZA World of Labor project is committed to the IZA Guiding Principles of Research Integrity. The author declares to have observed these principles.
© Jo Blanden