Counting on count data models

Comparing linear models and count data models

In a linear model, the range of the dependent variable is typically taken to be the set of real numbers; in a count data model, it is the set of natural numbers including zero. In a linear regression model, slope coefficients indicate the absolute change in the expected outcome associated with a unit change in x (for example, from x0 = 0 to x1 = 1), whereas in a count regression model with exponential conditional mean function, coefficients give the relative change in the expected outcome associated with a unit change in x. Consistent parameter estimation in both cases relies solely on a correctly specified mean function.

While the robustness and generality of the ordinary least squares estimator for the linear model is well understood, it is perhaps less well known that the non-linear Poisson maximum likelihood estimator, as an instance of pseudo maximum likelihood estimation, has similar properties [2]. Such robustness is of great practical relevance, as it means that the estimators for the parameters in the Poisson regression model are consistent even if the assumption for the distribution is incorrect, as is often shown to be the case.

It also follows that the Poisson regression can be applied even when the dependent variable is not a count at all, but rather some continuous non-negative variable, such as a duration, a wage, or a price. An example is the application of Poisson models to estimate gravity equations for international trade [3]. An important caveat when using Poisson regression in such contexts (when the mean is assumed to be correctly specified but the distribution is potentially wrong) is that the usual formula for the standard errors is wrong. In many cases, standard errors will underestimate the true variability in the estimator and thus lead to overly small confidence intervals and inflated t-statistics. However, a simple adjustment is available, leading to so-called “robust” standard errors, which ought to be routinely reported.

Why use count data models?

There are two main uses of count data models in policy evaluation. Often, the focus is on determining the effect of a policy change on the average count. Other applications exploit the fact that count data models yield predictions for the entire probability distribution. In a policy context, one can therefore determine the effect of the policy for each value of the outcome.

Figure 1 illustrates the situation in a hypothetical example using a Poisson model. It shows the predicted probabilities of the outcomes 0, 1, 2, etc., without the policy and with the policy. In this example, the outcomes are the number of doctor visits during a quarter (as an indicator of demand for health services), and the policy measure is the abolition of all co-payments and deductibles, that is, full insurance.

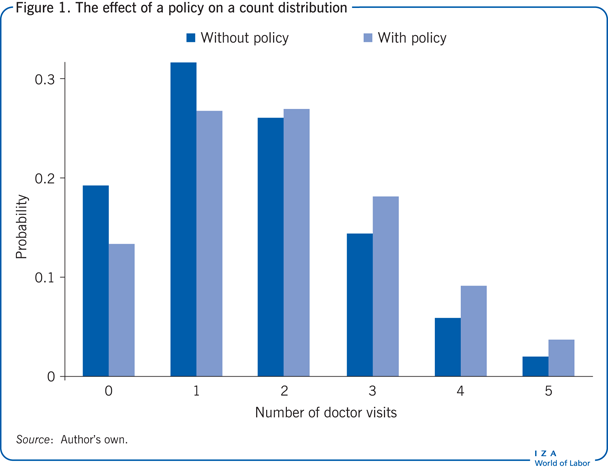
The computations in Figure 1 assume 1.65 average visits without the policy and 2.0 with the policy. Hence, the policy is associated with an increase in the mean outcome of about 2.0/1.65 – 1 = 21%. On the other hand, the policy is also associated with a 5.8 percentage point decline in the probability of zero usage. For a Poisson model, the probability of a zero is simply computed as the exponential of the negative mean, which is 0.192 in the case without the policy and 0.135 in the case with it. Similarly, a Poisson probability function can be used to show that the probability of a one decreases by five percentage points and the probability of a four increases by four percentage points.

To the extent that policymakers are interested not only in the average effect of a policy, but also in its distributional consequences, this can be very useful information. However, results are closely tied to the underlying assumption of the parametric distribution model—in this case, the Poisson distribution—and the plausibility of such analyses thus crucially depends on the validity of this underlying assumption. Tests and alternative specifications are discussed below.

Researchers sometimes choose a compromise between a fully-fledged distributional analysis and consideration of mean effects only by distinguishing between extensive and intensive margin effects. Extensive margin effects refer to the effect of a policy on the probability of zero usage (non-usage), whereas intensive margin effects refer to the effect of a policy on the mean, conditional on the count being positive. The classic example would be the distinction between the effect of a wage tax change on the labor force participation decision on the one hand and on the decision by workers on how many hours to work on the other. Both extensive and intensive margin effects can be readily obtained for any count data model. Of particular interest in this context is the hurdle model, which treats the process of zeros differently from that of non-zero counts. Adding this extra flexibility is important in many applications.

Which count data model?

For all purposes beyond robust estimation of the exponential regression model, the count data approach forces the researcher to commit to a particular parametric distribution. An informed choice should be based on the putative properties of the underlying data-generating process. For instance, if events occur completely randomly over time with constant probability, the Poisson model is appropriate. Such underlying randomness can be a reasonable assumption in the context of, for example, traffic accident frequencies. It is less satisfying in other contexts, such as worker absences, that are known to be more likely to occur on a certain day of the week [4].

The absenteeism example likely suffers from two further departures from the Poisson assumption. First, the chances of an absence tomorrow is higher for workers who were absent today. This is an instance of “occurrence dependence.” Second, workers are likely to differ in their intrinsic absence rates, with some workers being more likely than others to miss a day. This may depend on soft personality factors such as conscientiousness, but also on the family situation, for instance, if the worker has young children at home. If unobserved, these influences lead to so-called “unobserved heterogeneity.” Both occurrence dependence and unobserved heterogeneity invalidate the assumptions underlying the Poisson model. Unobserved heterogeneity leads to “overdispersion”: in the conditional model for y as a function of x, the variance increases overproportionally with the mean.

While the problem of occurrence dependence is not easily resolved, a powerful way to address unobserved heterogeneity arises whenever repeated observations on the same unit, or panel data, are available. For example, if there are data on the annual number of absences by a worker for several years, individual differences in absence propensities can be modeled directly, by including individual specific fixed effects. The panel Poisson regression model is easy to implement and shares many of the features known from the linear panel data model [5].

Alternative models can be derived under specific assumptions. For instance, a negative binomial model can be shown to arise as a consequence of either unobserved heterogeneity or occurrence dependence. If data are overdispersed, that model yields better predictions of the outcome probabilities. In particular, it predicts a higher proportion of zeros than does a Poisson model with the same mean. If the probability of an event increases or decreases with the time since the last occurrence, a gamma-count model may be appropriate [6].

Hurdle models combine a binary probability model, which determines whether the outcome is zero or strictly positive, with a parametric specification of the conditional-on-positives distribution [7]. Estimation using maximum likelihood proceeds in two steps, first using all observations for the binary response model and then using the subset of positive observations to estimate a truncated-at-zero count data model. Hurdle models can account for any degree of “excess zeros” and furthermore allow for an unrestricted estimation of extensive and intensive margin effects.

A related class of models with similar properties has frequently been used in applied health economics. Zero-inflated count data models assume that the data come from two distinct populations: one population that never experiences the event, and another one for which events are generated from a standard model. There are two types of zeros in such models, one stemming from the “never” population and the other from the “standard” population [7].

Non-random sampling is another issue arising in applied work. Unadjusted maximum likelihood estimation can lead to wrong inferences in such cases. Examples include truncation (as when observations with zero counts are not included in the sample), censoring (as when a survey asking for the number of children uses response categories such as “four or more” or reports on the “total” number of children for women under the age of 45, who may have more children later), and endogenous choice-based sampling (as when people with a large number of events are overrepresented in the sample) [8]. Since count data models fully specify the population distribution, it becomes quite straightforward to deal with such departures from random sampling in order to obtain consistent estimates of the population parameters.

Example: Application to the study of fertility

A natural application of count data models is in the analysis of fertility, as measured by the number of children ever born to a woman or the number of living children in a household. Modeling fertility encounters a number of interesting methodological challenges. In no particular order, these include the frequent presence of underdispersion (see [6]), the influence of infertility rather than individual choice on childlessness, and accounting for the fact that women surveyed may not yet have reached their completed (total) fertility.

The most radical approach for dealing with incomplete fertility excludes younger women, say those aged 45 or younger, altogether from the analysis. This approach has a couple of drawbacks, though. First, the omission of data on the current child-bearing generation results in a substantial lag in the collection of evidence on fertility patterns. This lag becomes more of a problem if fertility behavior is changing rapidly across cohorts. Second, the approach cannot be used if the number of children is based on household composition data, as children typically leave the household once they reach adulthood. In response, it is advantageous to include all women but to treat the number of children for younger women as a lower bound of completed fertility. A corresponding censored probability model is relatively simple to establish in the context of a parametric count data model. A parametric model can also be modified to allow for a culturally determined preference for two children, leading to “two inflation” observed in many data sets.

The example in Figure 2 shows the total fertility rates over the last 40 years for two countries, Germany and the US, as well as the average for OECD countries. Total fertility rates are computed by summing the age-specific fertility rates observed in a given year to obtain the number of children for a hypothetical women whose fertility over her lifetime is equal to the realized fertility rate for women of different ages in that year. The period 1970–2010 witnessed a marked decline in fertility, from 2.03 to 1.39 children per woman for Germany and from 2.76 to 1.74 for the OECD average; in the US the fertility rate stabilized around the replacement level after 1980.

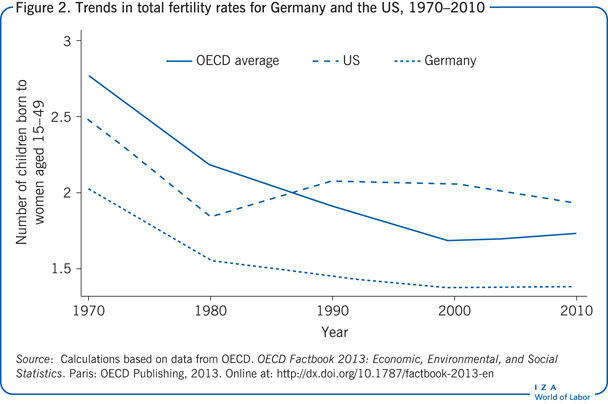
Clearly, policymakers are interested in the causes for such a decline, and many studies have been conducted to sort out the relative contributions of labor market developments, longer education periods (and thus a higher age at first childbirth), to name but a few. An illustrative analysis using data on completed fertility from the US General Social Survey for 1974−2002 shows how count data models can be used in this context. Based on 5,150 observations on women past childbearing age, the average number of children was 2.59, 14.5% of women were childless, and the modal number of children (the number that appears most often) was two (26.6% of all women). A simple Poisson regression including only a linear time trend gives a coefficient of –0.01. A test provided by [9] yields evidence of some overdispersion. Hence, robust standard errors should be used. In this case, the trend is statistically highly significant, and according to the model the average number of children declined by approximately 1% a year during this period.

One question to consider is the contribution of changing socio-demographic conditions to this secular trend. After controlling for years of schooling and indicators for race (white = 1), low income (family income below average at age 16 = 1), living in a city at age 16, and migration status, the new estimate of the trend component is a 0.55% annual decline in fertility, in this case 55% of what it was without accounting for schooling, race, income, urban residence, and migration status. The other 45% of the decline is explained by these factors. At the extensive margin, the Poisson model predicts that the probability of being childless has increased 2.9 percentage points over the 26-year-period for a mother with otherwise unchanged characteristics.

Estimating a linear regression model instead yields a predicted absolute effect of a –0.014 annual decline in fertility, the equivalent of one child less every 70 years. In contrast to the Poisson model, the linear model implies varying relative effects, because for a given absolute change, the larger the predicted mean, the smaller the relative change. Taking the sample average over the implied relative effects yields an estimated 0.58% decline in the number of children each year. In this example, the average relative effect implied by the linear regression model is similar to the effect estimated from the Poisson model, but this does not need to hold in general. Note that practitioners wanting to estimate a constant relative effects model often use the linear regression model after having transformed the dependent variable by taking logarithms. This is not possible here, as the outcome variable is zero for a sizeable fraction of the data.

Example: Application to demand for health services

The German health care system, like that of most other countries, has experienced many policy changes in recent decades. Examples include spending caps for doctors, privatization of hospitals, introduction of diagnosis-related groups for hospital reimbursement, and new cost-sharing arrangements for users. Around 90% of the German population receive their health insurance coverage through the German statutory health insurance system. Reforms that have been analyzed using count data models include a 1997 reform that increased co-payments for prescription drugs and a 2004 reform that introduced a co-payment for doctor visits. Both reforms had the professed objective of containing the rate of increase of health care expenditures by reducing demand for unnecessary medical treatment.

The 1997 reform increased the out-of-pocket cost of prescription drugs by a fixed amount. The relative effect of the 1997 reform was largest for small package sizes, where it amounted to a 200% increase. Social considerations resulted in several exemptions (for co-insured children and low-income households, a maximum cumulative annual co-payment limit of 2% of annual gross income and 1% for the chronically sick), generating potential control groups in addition to the privately insured.

One way to assess the effectiveness of such reforms is to deduce policy responses in behavior from household survey data, such as the German Socio-Economic Panel. While such surveys are not tailored to provide information on health-related issues, there is usually some limited information on health insurance status (private or statutory) and on health care use (such as the number of hospital admissions and number of doctor visits during the three months prior to the annual interview). For the 1997 reform, one would ideally study the change in demand for prescription drugs, but this information is not available in the survey data. However, because prescriptions require doctor visits, the analysis could focus on the indirect cost-saving effects of potentially fewer doctor visits instead [9].

Since the number of visits is a count, quantitative evaluations of the effect of these reforms on demand for health services can employ count data models, using either pre-reform and post-reform comparisons or a difference-in-differences analysis [9], [10]. For instance, to analyze the effect of the 1997 reform, German Socio-Economic Panel microdata for two years can be used, with 1996 data for the pre-reform period and 1998 data for the post-reform period. Respondents with statutory health insurance can be considered the treatment group and those with private insurance the control group. The control group establishes a baseline counterfactual trend in doctor visits pre- and post-reform, due, for example, to changes in general economic conditions. Any deviation from this baseline trend observed for the treatment group is then assumed to reflect the effect of the reform.

For these health care reforms, as for others, there are good reasons to believe that not every affected person responds in the same way to the reform. In particular, extensive and intensive margin effects might differ—in this case, the effect on any visit compared with the effect on the non-zero number of visits. In the case of the 1997 reform, the chronically ill likely had less leeway to respond in order to avoid co-payments compared with people who were in good health. One would therefore expect a lower sensitivity to the reform at the intensive margin, in the right part of the outcome distribution, than at the extensive margin.

To address this issue, a study estimated various count data models and indeed found evidence of a differential response [10]. Based on hurdle models, the predicted probability of being a prescription drug user (at least one doctor visit) decreased an estimated 6.7% between 1996 and 1998, whereas the expected number of visits, conditional on use, decreased only an estimated 2.6%. In contrast, a simple Poisson model without hurdle leads to quite different effect estimates, a 3.0% decline at the extensive margin (as opposed to a 6.7% decline in the hurdle model) and 6.1% decline at the intensive margin. This illustrates a substantial bias of the standard Poisson model and highlights the need for a model with sufficient flexibility.