Elevator pitch
Often, economic policies are directed toward outcomes that are measured as counts. Examples of economic variables that use a basic counting scale are number of children as an indicator of fertility, number of doctor visits as an indicator of health care demand, and number of days absent from work as an indicator of employee shirking. Several econometric methods are available for analyzing such data, including the Poisson and negative binomial models. They can provide useful insights that cannot be obtained from standard linear regression models. Estimation and interpretation are illustrated in two empirical examples.
Key findings
Pros
Count data regressions provide an appropriate, rich, and flexible modeling environment for non-negative integers, 0, 1, 2, etc.
Poisson regression is the workhorse model for estimating constant relative policy effects.
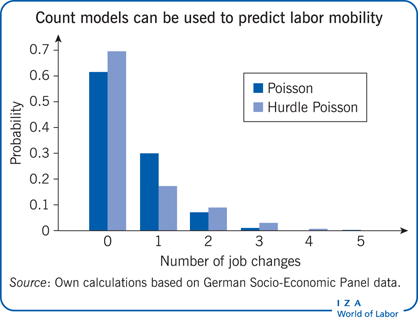
Hurdle and related models allow distinguishing between extensive margin effects (outcome probability of a zero) and intensive margin effects (probability of one or more counts).
With count data, policy evaluations can move beyond the consideration of mean effects and determine the effect on the entire distribution of outcomes instead.
Cons
Count data models impose parametric assumptions that, if invalid, can lead to incorrect policy conclusions.
While many software packages implement standard count models, such as the Poisson and negative binomial models, more elaborate models may require some programming by the researcher.
A count data approach does not solve the fundamental evaluation problem: absent a randomized controlled experiment, identifying policy effects from observational data can be marred by selection bias, requiring plausibly exogenous variation in the form of a quasi-natural experiment.